Introduction
In this article, I will demonstrate how to run an elementary Monte Carlo experiment on Azure Batch. More specifically, we are going to estimate π.
☝🏻 Throughout this post, I assume a basic understanding of Azure Batch. For an introductory read, please refer to the official documentation.
There are three variants for calculating π in a probabilistic manner, these are:
- The unit-circle/unit-square method
- The integral way through the calculation of the average of functions
- Buffon's needle problem
There are more efficient methods to calculate π than the one we will use here (e.g., Spigots algorithm). However, we are going to stick with the first one, as it is easy to follow and well-known.
If you would like to know more about the mathematical details, this blog post by Maike Elisa provides excellent explanations, which you can find here.
Estimating π with a Monte Carlo experiment can be solved intrinsically parallel, meaning worker tasks do not have to exchange information. Each instance can complete part of the work on its own. This approach allows to run the workload at a large scale and reduce code complexity.
This type of workload contrasts to so-called tightly coupled workloads, where tasks need to communicate with each other (usually via Message Passing Interface, MPI). Some example workloads are fluid dynamics, finite element analysis, and others. However, these are problems we are not going to deal with in this article.
Before we jump in and start with some math 🤓👨🏻🔬 here is the link to the repository. The exemplary code is written in .NET Core/C#.
Mathematical background
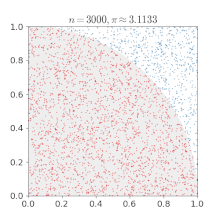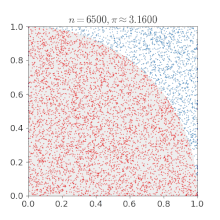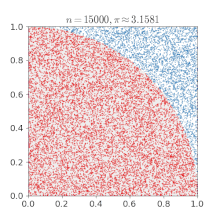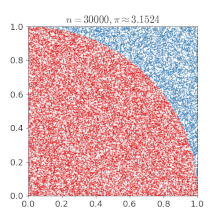
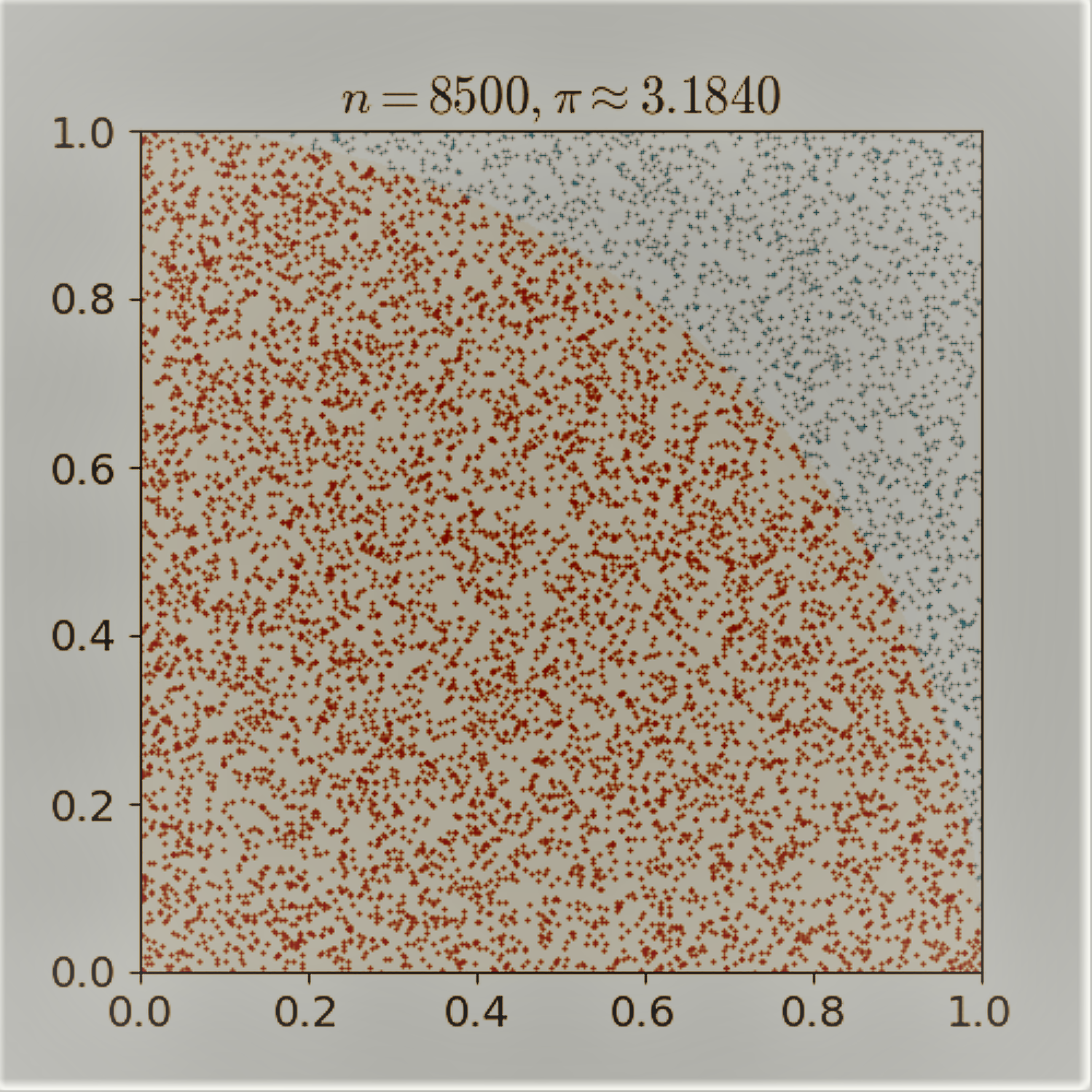
To determine π, we are going to create a massive amount of random points on a plane that encloses a unit circle, where (x, y|x ∈ [-1..1] ∧ y ∈ [-1..1]).
Then we will test if they fall in the unit circle by using Pythagoras' theorem x² + y² ≤ 1 and counting those hits.

As the circle's area can be calculated by A = r²π and the area of the square by A = (2r)², we can put them into proportion and then deduce π as follows.

How to parallel the problem?
Now that we would d like to solve the problem with Azure Batch, we need a way to break the problem apart into smaller pieces.
So let us cut the plane into stripes and let each worker node generate random points on its unit of work plane (the stripe). We also could have cut the plane into squares, but using stripes eases the splitting part.
In the following picture, we created working units for four nodes, where each will generate random points with (x0, y0|x0 ∈ [-1..-0.5] ∧ y0 ∈ [-1..1]) and (x1, y1|x1 ∈ [-0.5..0] ∧ y1 ∈ [-1..1]), etc...

Then, we add the number of circle hits on each of the units of work planes and divide it by the total number of random points generated, resulting in a rough estimation of π.
A more optimized approach to parallel the problem
The described approach to parallel the problem is a primitive one and not very efficient. By cutting the plane into stripes, we enclose huge areas known to be in the circle and therefore waste computation time.
Instead, we could divide the area into smaller squares. Then we would only generate random points on those sub-squares, which have an intersection with the circle (e.g., number 3).

For example, generating random points on sub-square number 1 does not make sense, as all would end up outside the circle. The same goes for sub-square number 2, where all points would end up in the circle. These sub-squares can be added as constants to the final summation.
If a sub-square requires computation (e.g., number 3), it could easily be tested by checking if at least one edge is in and another one outside the circle (test with x² + y² ≤ 1 for each edge).
So, the given example would reduce the number of areas from 64 to 28, which is a time (and money) saver! However, that exercise is left for some other rainy day.
The final solution
With the math being out of the way, we can now walk through the final application. This section is going to describe the components and only the most relevant parts of the workflow. These are:
- Uploading the chunked input data to the linked storage account
- Downloading input data (resource files) onto the nodes
- Performing the computation
- Uploading the computation output & logs to the linked storage account
- Monitoring and waiting for the tasks to finish
- Retrieving logs & results from tasks
Hopefully, the other parts of the source code are self-explanatory. Here is the link to the repository.
Components
The batch solution is following the blueprint architecture provided by Microsoft. It is consists of two main components, the Cluster Head, which controls the operations, and the Workload Runner doing the actual computation on the nodes.
☝🏻 Please do not get confused! Microsoft usually calls the Cluster Head just client, application, or service.

Cluster Head's responsibility
- Runs on a workstation
- Splits input data into chunks and uploads them to the storage account
- Creates a job and defines the tasks
- Monitors tasks for progress
- Collects partial results and aggregates them
Workload Runner's responsibility
- Runs on pool nodes
- Stored as an application package (manually uploaded)
- Gets triggered by each task
- Downloads input data (resource files) from the storage account
- Performs computation
- Uploads output (partial result) to the storage account
Uploading the chunked input data to the linked storage account
For splitting the data, I have a method that takes the total number of random numbers and units (input data for tasks) to generate.
public static IList<Unit> GenerateUnits(ulong iterationsTotal, uint unitsTotal)So when calling, e.g., var units = Tools.GenerateUnits(100, 4), we will get four units, where each will generate 25 random points. Next, the units are serialized and uploaded via UploadResourceFilesAsync that finally calls BlobContainerClient.UploadBlobAsync().
public async Task UploadResourceFilesAsync(IEnumerable<Unit> units, string containerName)I couldn't find a way to upload resource files directly via the Batch SDK. Please drop me a mail if you know of a more native way!
And eventually, the input files end up in the configured blob container as depicted.

Downloading input data (resource files) onto the nodes
There are three options available to download resource files onto the nodes, these are:
- Via any storage container
- Via the single auto-storage linked to the Azure Batch account
- Via any valid HTTP URL
I have chosen to go down the auto-storage route, as I would like to keep things as simple as possible.
Using the auto-storage container allows us to bypass configuring and creating a SAS URL to access the storage container. Instead, we only need to provide the name of the storage container, and we are good to go!
This is achieved by calling ResourceFile.FromAutoStorageContainer() at the time of task creation. Then, the resource file will end up in the task-specific working directory (e.g., wd\input-0.json) if nothing else was specified via the filePath parameter.
var task = new CloudTask(id, commandLine)
{
ApplicationPackageReferences = new List<ApplicationPackageReference>()
{
new ApplicationPackageReference { ApplicationId = "consumer", Version = "1.0.0" }
},
EnvironmentSettings = new List<EnvironmentSetting>()
{
new EnvironmentSetting("JOB_OUTPUT_CONTAINER_URI", this.outputContainerSasUrl)
},
ResourceFiles = new List<ResourceFile> { ResourceFile.FromAutoStorageContainer("input-files", blobPrefix: $"input-{i}.json") },
Constraints = new TaskConstraints(retentionTime: TimeSpan.FromDays(1)),
};
Performing the computation
After the consumer has read and deserialized the JSON input file, it generates the random points on the specific stripe and counts the circle hits.
public static bool IsInCircle(double x, double y) => x * x + y * y <= 1.0;
public static Unit GenerateRandomPoints(Unit unit)
{
var stopwatch = new Stopwatch();
stopwatch.Start();
var random = new Random();
ulong circleHits = 0;
for (ulong i = 0; i < unit.NumRandomPoints; i++)
{
var x = random.NextDouble() * (unit.Area.UpperX - unit.Area.LowerX) + unit.Area.LowerX;
var y = random.NextDouble() * (unit.Area.UpperY - unit.Area.LowerY) + unit.Area.LowerY;
if (IsInCircle(x, y))
circleHits++;
}
stopwatch.Stop();
unit.ElapsedMilliseconds = stopwatch.ElapsedMilliseconds;
unit.CircleHits = circleHits;
return unit;
}Uploading the computation output & logs to the linked storage account
For uploading the output data, we can choose between a couple of options, which are:
- Using the Batch Service API
- Using the Batch File Conventions library for .NET
- Implementing the Batch File Conventions standard in your app
- Implementing a custom file movement solution
I decided to use the second approach and go with the Batch File Conventions library, as it simplifies the process of storing task output and retrieving it.
At the same time, the library can be used on both the consumer for uploading output data and on the cluster head for downloading the results.
Also, I wanted to view the task output & logs from within the Azure Portal, which is made possible due to the convention.

The result of the computation is uploaded by the task itself, like so:
var jobOutputContainerUri = Environment.GetEnvironmentVariable("JOB_OUTPUT_CONTAINER_URI");
var taskOutputStorage = new TaskOutputStorage(new Uri(jobOutputContainerUri), taskId);
WorkloadRunner.UploadTaskOutput(unit, taskOutputStorage);As you might have noticed, the creation of the TaskOutputStorage() type requires a SAS URL, that I am creating on the Cluster Head and then pass down by an environment variable.
public async Task<string> GetOuputContainerSasUrl(ICloudJobWrapper job)
{
var storageAccount = this.clusterService.GetStorageAccount();
await job.PrepareOutputStorageAsync(storageAccount);
return job.GetOutputStorageContainerUrl(storageAccount);
}
public async Task<IEnumerable<string>> CreateTasksAsync(string jobId, IEnumerable<Unit> units)
{
...
this.outputContainerSasUrl = GetOutputContainerSasUrl(job)
var task = new CloudTask(id, commandLine)
{
...
EnvironmentSettings = new List<EnvironmentSetting>()
{
new EnvironmentSetting("JOB_OUTPUT_CONTAINER_URI", this.outputContainerSasUrl)
},
...
};
...
}Then, the method UploadTaskOutput() is finally calling TaskOutputStorage.SaveAsync() which allows classifying the kind of output we are saving.
public static void UploadTaskOutput(Unit unit, TaskOutputStorage taskOutputStorage)
{
...
// Copying log files to working directory to prevent locking issues
File.Copy(sourceFileName: $@"..\{Constants.StandardOutFileName}", destFileName: Constants.StandardOutFileName);
File.Copy(sourceFileName: $@"..\{Constants.StandardErrorFileName}", destFileName: Constants.StandardErrorFileName);
Task.WaitAll(
taskOutputStorage.SaveAsync(TaskOutputKind.TaskLog, Constants.StandardOutFileName),
taskOutputStorage.SaveAsync(TaskOutputKind.TaskLog, Constants.StandardErrorFileName),
taskOutputStorage.SaveAsync(TaskOutputKind.TaskOutput, @"output.txt"));
}Depending on the value of TaskOutputKind the data ends up in one of the following paths.
| TaskOutputKind | Path |
|---|---|
| TaskOutputKind.TaskLog | {task-id}/$TaskLog/ |
| TaskOutputKind.TaskOutput | {task-id}/$TaskOutput/ |
| TaskOutputKind.Preview | {task-id}/$TaskPreview/ |
| TaskOutputKind.Intermediate | {task-id}/$TaskIntermediate/ |

Monitoring and waiting for the tasks to finish
This can be done with the help of a TaskStateMonitor.
var batchClient = BatchClient.Create(...);
var monitor = batchClient.Utilities.CreateTaskStateMonitor();It provides two methods. First, there is WaitAll() which is blocking, and second the asynchronous counterpart WhenAll().
These methods take our tasks as input and further let us configure the desired state we'd like to wait for. Also, we can optionally define the polling delay and maximum time to wait.
var controlParams = new ODATAMonitorControl()
{
DelayBetweenDataFetch = TimeSpan.FromSeconds(3)
};
taskStateMonitor.WaitAll(tasks, TaskState.Completed, TimeSpan.FromMinutes(15), controlParams);
Retrieving logs & results from tasks
Last but not least, we are going to read back the files by leveraging again a TaskOutputStorage.
var taskOutputStorage = new TaskOutputStorage(new Uri(this.outputContainerSasUrl), taskId);
var stdout = await taskOutputStorage.GetOutputAsync(TaskOutputKind.TaskLog, Constants.StandardOutFileName);
var stderr = await taskOutputStorage.GetOutputAsync(TaskOutputKind.TaskLog, Constants.StandardErrorFileName);
var output = await taskOutputStorage.GetOutputAsync(TaskOutputKind.TaskOutput, "output.txt");The mighty results
Here are some test runs I did. The results show the huge amount of iterations required to reach a decent precision.
IterationsTotal: 1'000'000
UnitsToGenerate: 4
Nodes: 4
vCPUs: 4
Total calculation time: 00h:00m:00s:055ms
Total run time: 00h:00m:11s:333ms
Estimated PI: 3.1420560
Math.Pi: 3.141592653589793With 1'000'000 random points, we reached a precision of 2 decimal places.
IterationsTotal: 34'359'738'360
UnitsToGenerate: 4
Nodes: 4
vCPUs: 4
Total calculation time: 00h:33m:54s:936ms
Total run time: 00h:09m:48s:308ms
Estimated PI: 3.1415838323630354908208911052
Math.Pi: 3.141592653589793With 34'359'738'360 random points, we reached a precision of 4 decimal places.
IterationsTotal: 137'438'953'440
UnitsToGenerate: 16
Nodes: 6
vCPUs: 6
Total calculation time: 02h:13m:13s:804ms
Total run time: 00h:31m:46s:174ms
Estimated PI: 3.1415946968520513495551541796
Math.Pi: 3.141592653589793With 137'438'953'440 random points, we reached a precision of 5 decimal places.
IterationsTotal: 549'755'813'760
UnitsToGenerate: 16
Nodes: 2
vCPUs: 4
Total calculation time: 08h:59m:13s:381ms
Total run time: 02h:21m:47s:118ms
Estimated PI: 3.1415927164746315024035590472
Math.Pi: 3.141592653589793With 549'755'813'760 random points, we reached a precision of 6 decimal places.
Further thoughts & questions
Here are some unsorted questions, ideas & thoughts that came up during the work on this article. They might be incorporated in further posts.
Lessons learned & thoughts
- The cluster head code currently doesn't allow re-attaching to the service and needs to be running during computation. However, this could easily be fixed by some slight modifications.
- Create an Alert on the Batch Service, to get notified when a (long-running) job has been completed.
- When using low-priority nodes, it's better to choose virtual machine sizes with fewer cores, as this will leave you with the most available vCPUs in the pool, in case a pre-empting is happening.
- When dealing with huge numbers, it's even more important to unit-test edge cases.
- Mocking Azure Batch type can be painful (needs a lot of wrapping), e.g. CloudJob, CloudPool, BatchClient, ...
- To progressively get premature results, asynchronous messaging (Service Bus, Storage Queues) and Azure Durable functions could be leverages.
Questions
- How can the experiment prematurely be stopped in case a required precision has been reached? When will the algorithm converge?
- How to choose the right node size (performance vs. cost)?
- How can we auto-resize a static pool, in case a low-priority node gets preempted?
- Coming up with an efficient thread & task (TPL) design on the worker node can be difficult. How much work should be left to the Azure Batch Scheduler?
- Could this experiment be run more efficiently on Azure Durable Functions and a fan-out/fan-in pattern?
Conclusion
Wow, that was an exciting journey 😄. Writing this article took me (a lot) longer than I originally envisioned, it's easy to get carried away by details 🤪. However, the learnings I took were worth it.
I hope you enjoyed reading this article and I would be glad to receive feedback & improvement proposals. Happy hacking! 👨🏻💻
Further reading & links